Blog

PQC or Post Quantum Cryptography
A summary of the current state of play in the field of quantum computer-resistant cryptography, along with simplified explanations of attacks on current algorithms, overviews of problems, and the importance of individual technologies.
Quantum computer-resistant algorithms
It is quite challenging to understand the terms used to denote the current development in the field of cryptography. But it is necessary especially because of the imminent emergence of quantum computer technology. The development of these machines has given new impetus to the development of cryptography. At the same time, they are popularly referred to as cryptographic Armageddon, the death of classical cryptography and other catchy terms. Quantum computers can cause inconvenience to existing technologies which involve e.g. agreeing on encryption keys or digital signatures, but they can pose a threat to other current encryption techniques. The reason is simple, it is now possible to collect data and decrypt them when those machines become available (HNDL = Harvest Now, Decrypt Later). There are secrets, even of an economic nature, that need to be protected for a longer period of time. Longer period in that case means years or tenth of years.
Current cryptography has a powerful tool in its arsenal, asymmetric cryptography. Asymmetric, because the keys are used asymmetrically. Private key for encryption, public key for decryption (or vice versa, depending on the purpose). Those algorithms are known under names RSA, ElGamal, Schnor signature, DSA, or cryptography over elliptic curves (ECDH/ECDSA). The user always has a pair of private and public key, where the public key is derived from the private key. These methods are used for agreeing on shared secrets (protecting our communications within SSL/TLS, SSH, IPSec and other technologies) or for digital signatures. The first algorithms for asymmetric cryptography, which provides these areas, appeared in the 1970s. The first practical deployment was a decade later. Now, after 40 years of development, we have managed to eliminate the biggest problems, to start using these technologies. Although these are in most cases trivial procedures, based on elementary and high school teaching, some of the problems are extremely interesting and are still not unequivocally solved. With current asymmetric algorithms, the impact of quantum computers is devastating. This was caused by an idea by Peter W. Shor, who suggested using first the search for a modular base number for factorization. For this purpose, it is possible to use a quantum version of the Fourier transform (the mathematical version of "period measurement"). And the only defense option is to find new, quantum computer-resistant procedures.
| Algorithm | Attack time |
| RSA 1024/DH 1024 | 3,5 day |
| RSA 2048/DH 2048 | 7 day |
| RSA 3072/DH 3072 | 10,6 day |
| ECDH 256 | 3,1 day |
| ECDH 384 | 4,7 day |
| ECDH 512 | 6,3 day |
Current symmetric cryptography (the key is used symmetrically = the same key is used for both encryption and decryption) is built over block ciphers such as AES, ARIA, CAMELLIA, or stream ciphers such as ChaCha20. To list them this article would not suffice. The algorithms listed represent a method of securing large volumes of data because they are relatively fast. Quantum computers bring inconvenience, these encryption algorithms may be threatened by a Groover attack if small keys are used (i.e. smaller than about 168b, because of protection recommended to use at the least are 192b with minimal security reserve), but is this not a false alarm? The answer is simple, it is not. Although the Groover algorithm is nothing more than an effective way of searching unsorted databases. In the case of a quantum computer, there are two possible ways for an attack. Either create a huge database of all combinations of open text, keys and encrypted text, or combine the search and encryption algorithms into one more complex one.
If the Groover and encryption algorithms are combined, e.g. with the implementation of AES for quantum computers, we should get a powerful tool. Theoretically, such a solution should return the information immediately. Calculations vary, for a key of size 128b, it should be an interval from 8 minutes to 30 years (depending on the design of the whole device, whether it would be a specialized circuit or a general quantum computer with a program). But for a key of size 192b, it would be time consuming at least 40,000 years. Therefore, it is necessary to use a larger key material in order to move the attack from the practical to the theoretical level. Of course, this is a theoretical attack for now, because we do not have the equipment for it yet and only parts of the algorithm have been tested. The important thing is to choose the length of the key so that it protects secrets with reserve for the required time, e.g. several decades.
For the sake of interest. If we only want to create a database of keys and encrypted texts for a key the size of 128b, we are outside the technological and raw material possibilities. If a memory cell would require 100 silicon atoms (and some doping elements), without any other supporting circuits, the storage would have a radius of 5000 AU … and would immediately collapse into a black hole due to its weight and gravitational action. So this is not the way, such a solution can only be taken as a cryptographic attack and a mathematical game play.
Post-quantum cryptography competitions
Currently, in late 2024, the following contests are taking place to select quantum-resistant algorithms. These are often referred to as PQC – Post Quantum Cryptography. Based on the outcome of these contests, it is advisable to prepare the transition to quantum-computer-resistant cryptography. A rough idea for the transition may look like the following, depending on client requirements. Support for algorithms with 128b security equivalent is to be discontinued in 2030 and support for hybrid algorithms should be discontinued by 2035 at the latest.
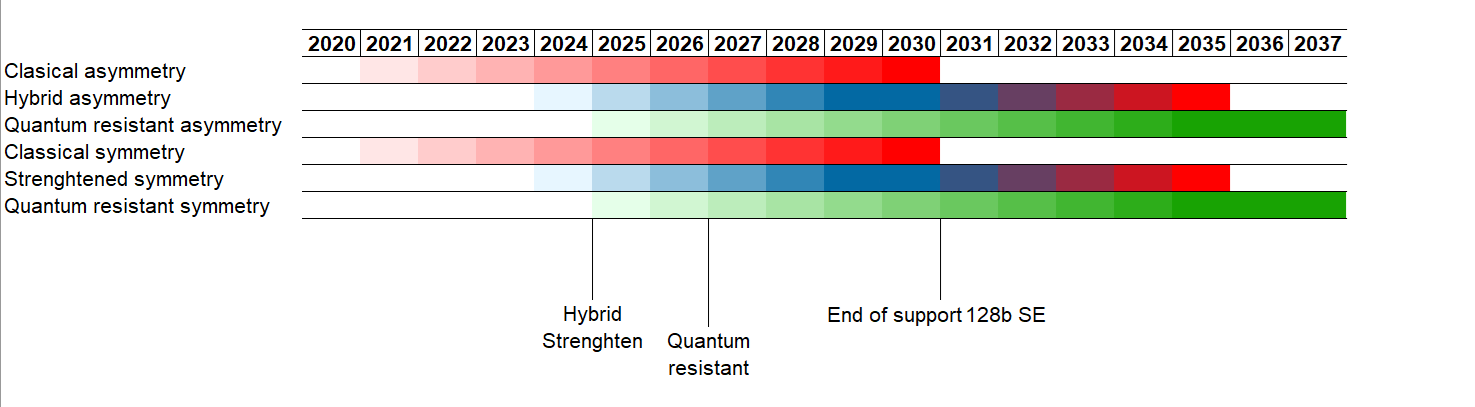 |
1 - Start migration projects on PQC / QRC
2 - Start custom migration
3 - End migration for quantum-resistant key exchange cryptography on CI (Critical Infrastructure)
4 - End migration to quantum-resistant key exchange cryptography
- End support for symmetric algorithms with security equivalent < 192b
5 - End migration to quantum-resistant cryptography for digital signature
NIST Post Quantum Cryptography (USA)
The results of this competition are generally accepted in Canada, Europe, the Middle East, parts of Asia, Japan,
Australia and other places. More information about this competition can be found at addresses:
NIST Post Quantum Cryptography
NIST Post Quantum Cryptography: Additional Digital Signature Schemes
This is a local matter, with experts such as Tanja Lange acting as independent gestors. Thanks to the export of scientific and cultural trends (soft power), this activity will probably have some, at present difficult to predict impact, but will certainly be used by Samsung, LG, KIA/Hyundai... More information about this competition can be found at KpqC competition
CACR PQC standardization - Chinese Association for Cryptography Research Post Quantum Cryptography (China)China is trying to demonstrate its independence in this area as well. Recently I came across information that Russia should be interested in cooperating on this development, but the information is scarce and for me it is difficult to read. More information about the competition can be found at CACR PQC standardization
Standards with an impact on Europe
Europe is determined by ETSI standardiation(
European Telecommunications Standards Institute), it also has an interesting and generally accepted result of NIST PQC,
which has already created three standards, the fourth is in the design stage. According to the current situation, there will
be enough algorithms for a digital signature, but probably not enough to provide an alternative to agreeing on a shared
secret. But this is necessary to maintain the possibility of agreeing on keys and
to ensure the confidentiality of encrypted communication.
FIPS 203 ML-KEM (originally Crystal Kyber, Key Encapsulation Mechanism, SVP+LWE)
FIPS 204 ML-DSA (originally Crystal Dilithium, Digital Signature Algorithm, SVP+LWE)
FIPS 205 SLH-DSA (Stateless Hash Based DSA, Digital Signature Algorithm, uses stateless
hash trees)
In addition, the listed algorithms have a recommended security level, called NIST Security level:
Security level 1, security equivalent 128b (AES-128, exhaustive key search)
Security level 2, security equivalent 128b (SHA-256, collision search)
Security level 3, security equivalent 192b (AES-192, exhaustive key search)
Security level 4, security equivalent 192b (SHA-384, collision search)
Security level 5, security equivalent 256b (AES-256, exhaustive key search)
More interestingly, what recommendations each organization makes about the given standards. In my opinion
it is still unclear how to approach the given standards. Due to the difficulty of analyzing the complexity of an attack
conversion to a security equivalent is still a problem. Here is an overview of the digital signature algorithms:
| Organization | Digital Signature | Digital Signature | Other DSA |
| CNSA 2.0 (USA) | ML-DSA level 5 | LMS/XMSS | |
| NIST (USA) | FIPS 204 (ML-DSA) | FIPS 205 (SLH-DSA) | FN-DSA |
| NCSC (UK) | ML-DSA level 3 | LH-DSA/LMS/XMSS | |
| BSI (Germany) | ML-DSA Levels 3/5 | SLH-DSA Level 3/5 | LMS/XMSS |
| NLNCSA (Netherlands) | ML-DSA | LMS/XMSS | |
| ANSSI (France) | ML-DSA level 3 | SLH-DSA Level 3/5 | FN-DSA/LMS/XMSS |
| NUKIB (Czech) | ML-DSA level 3/5 | SLH-DSA Level 3/5 | FN-DSA/LMS/XMSS/SLH-DSA |
| (South Korea) | KpqC competition | KpqC competition | |
| (China) | CACR PQC standardization | CACR PQC standardization | |
| IETF | LMS/XMSS |
Digital signature is important for authentication, electronic communication, or from the point of view of the law as a manifestation of the will. But digital signature alone is not able to ensure the protection of transmitted information, or even to agree on key material (shared secrets). There are other algorithms for that, more precisely only one for now algorithm:
| Organization | Key Exchange | Other Key Exchange |
| CNSA 2.0 (USA) | ML-KEM Level 5 | |
| NIST (USA) | FIPS 203 (ML-KEM) | |
| NCSC (UK) | ML-KEM Level 3 | |
| BSI (Germany) | ML-KEM Level 3/5 | FrodoKEM/McEliece |
| NLNCSA (Netherlands) | ML-KEM Level 3 | FrodoKEM |
| ANSSI (France) | ML-KEM Level 3/5 | FrodoKEM/McEliece |
| NUKIB (Czech) | ML-KEM Level 3/5 | FrodoKEM/McEliece |
| (South Korea) | KpqC competition | |
| (China) | CACR PQC standardization | |
| IETF |
It is the Key Exchange Method (KEM) algorithms that can also force changes in current protection methods. SSL/TLS protocol is most often used, followed by SSH protocol. Both layers have a somewhat similar architecture and protocol structure. It is with SSL/TLS that there is a risk that certificates with key material signed by post-quantum algorithms may exceed the size of the record. This can be transmitted by multiple packets, but must be smaller than 18432B (214 + 2048). If the certificate or certificate chain is longer, the connection will be interrupted. And some proposed KEM algorithms may have key material extremely extensive.
Beyond the above algorithms, so-called hybrid algorithms have emerged, more or less temporarily. These are built over a combination of classical and post-quantum algorithms and are intended to act as protection should any of the above mechanisms experience a significant security threat. They are currently used in SSL/TLS and SSH, these hybrid algorithms include:
| Název | Algoritmy |
| ecdh-nistp256-kyber-512r3-sha256 | NIST P-256 + Kyber-512 + SHA256 |
| ecdh-nistp384-kyber-768r3-sha384 | NIST P-384 + Kyber-768 + SHA384 |
| ecdh-nistp521-kyber-1024r3-sha512 | NIST P-521 + Kyber-1024 + SHA51 |
| x25519-kyber-512r3-sha256 | Curve25519 + Kyber-512 + SHA256 |
| x25519-kyber-768r3-sha256 | Curve25519 + Kyber-768 + SHA256 |
Problems allowing the creation of asymmetric algorithms
In terms of methods used in the creation of classical asymmetric is available the following a set of problems. These are currently at their peak and will need to be replaced by another set in the foreseeable future, able to withstand quantum computers:
| FACTORING | Integer Factorization Problem |
| RSAP | RSA problem (RSA inversion) |
| QRP | Quadratic Residuosity problem |
| SQROOT | Search for the square root that forms the number modulo base (Square roots modulo n) |
| DLP | Discrete Logarithm Problem |
| GDLP | General Discrete Logarithm Problem |
| DHP | Diffie-Hellman Problem |
| GDHP | General Diffie-Hellman Problem |
| SUBSET-SUM | Subset Sum problem |
In the case of algorithms resistant to quantum computers, it was necessary to find a completely different set of problems. Previous the set of problems was not sufficiently resistant to new technologies, so it was necessary to look for something better. Such procedure is a normal part of development and of course cryptography does not remain stationary. Some of these procedures are about the same age as current asymmetric cryptography, some are part of the evolution of recent decades. For the new algorithms they used the following groups of interesting problems:
| Lattice-based cryptography | Shortest Vector (SVP) Search Shortest Independent Vector (SIVP) Search Find the closest vector (CVP) Learning with errors (LWE) problem Short integer solutions (SIS) ...their combinations. |
SVP+LWE problem - FIPS 203 ML-KEM SVP+LWE problem - FIPS 204 ML-DSA SVP+LWE problem – e.g. Frodo, Glyph, NewHope, TESLA CVP – e.g. NTRU, BLISS |
| Linear codes Code-based cryptography |
Problem decoding general linear code SDP Syndrome Decoding Problem RSDP Rank Syndrome Decoding Problem |
Examples are McEliece, BIKE, HQC and others |
| Solution of system of nonlinear equations Multivariate cryptography |
Examples are OAV (Oil and Vinegard), GeMSS, Rainbow ... | |
| Hash trees Hash-based cryptography HBS:Hash Based Signature |
Status trees Status trees LMS (Leighton-Micali Scheme) XMSS (eXtended Merkle Signature Scheme) status trees FN status trees (Fast-fourier transform over NTRU-lattice) |
FIPS 205 SLH-DSA (Stateless Hash Based DSA) draft FIPS 206 FN-DSA (Falcon) |
| Supersingular curves with invariants Supersingular isogeny-based cryptography |
General Model Comutative Model |
SIDH CSIDH (Commutative Supersingular Isogeny Diffie-Hellman) |
| Other interesting problems | Search problem Braid groups (operations in braid groups) Complex algebra over octonions Complex algebra over sedenions Chebyshev polynomials (Chebyshev polynomials) |
Conclusion
Current algorithms will be seriously compromised by 2030-2040 and it is necessary to prepare for the impacts that quantum
computers bring. On the other hand, it is necessary to be careful, premature implementation can create a problem in itself.
The reason for this precaution is simple. It took us 40 years to create functional asymmetric cryptography
built over quite simple problems, actually over the curriculum of primary and secondary schools. New approaches require
substantially deeper mathematical knowledge, evidence of correctness and only developments in mathematics will answer the question whether they are
the procedures chosen are correct. The individual steps should therefore, in my opinion, be approximately as follows:
1. Increase key size for symmetric algorithms to 192b (25% higher load than 128b), better to 256b
(25% higher load than 192b). This makes it easy to avoid problems with the possibility of attack by Groover's
algorithm.
2. Switch to hybrid algorithms by 2024 at the latest, unless switching directly to quantum-resistant algorithms.
However, hybrid algorithms will not be suitable for use beyond 2030-2035 and at the latest must be
replaced by tested quantum-resistant algorithms. This trip is for paranoids who either have concerns
possible weaknesses of new algorithms, or kleptography (design allowing unauthorized access to information)
for new standards.
3. Start within two years of standardization, or at most within five years of standardization to complete the transition
on quantum-resistant algorithms. Both for the agreement on the keys and for the digital signature. In the case of digital
signature, this will mean significantly more changes in different systems.
Attachments: List of libraries supporting quantum cryptography
BoringSSL is a Google fork of OpenSSL. Library is implemented in Chrome and Chromium browsers
as well as Android operating system.
https://boringssl.googlesource.com/
Botan is an opensource library in C++. It supports Unix/POSIX and Windows systems. More information on
GitHub
liboqs is an opensource library in C. It supports Linux, Mac and Windows through the
"Open Quantum Safe Provider for OpenSSL" library. More information on
GitHub
SymCrypt is a Microsoft library under an MIT license. It supports both the new CNG API,
and the older CAPI we Windows. In Linux, you can call SymCrypt APIs directly or through interfaces,
for example, the OpenSSL interface.
GitHub
Attachments: List of algorithms in the NIST PQC
List of algorithms in the NIST competition, including their download, disable, merge, or standardization. This list is still incomplete and the goal is to fill in the missing data to allow a preview of the entire development.
| Algorithm | Goal | Problem | Type | Submission | Round 1 | Round 2 | Round 3 | Round 4 |
| BIGQUAKE | KEM | Codes | Goppa | Discard | - | - | - | |
| BIKE | KEM | Codes | Short Hamming | BIKE | BIKE | |||
| CFPKM | KEM | Codes | RSDP | Discard | - | - | - | |
| Classic McEliece | KEM | Codes | Goppa | Classic McEliece | Classic McEliece | Classic McEliece | ||
| CompactLWE | KEM | Lattice | LWE | Discard | - | - | - | |
| CRYSTALS-DILITHIUM | DSA | Lattice | Fiat-Shamir | FIPS-204 | ||||
| CRYSTALS-KYBER | KEM | Lattice | MLWE | FIPS-203 | ||||
| DAGS | KEM | Codes | Quasi dyadic | Discard | - | - | - | |
| Ding Key Exchange | KEM | Lattice | RLWE | Discard | - | - | - | |
| DME | ? | Multivariate | UOV | Discard | - | - | - | |
| DRS | DSA | Multivariate | UOV | Discard | - | - | - | |
| DualModeMS | DSA | Multivariate | UOV | Discard | - | - | - | |
| Edon-K | KEM | Codes | Withdrawn | Discard | - | - | - | |
| EMBLEMandR.EMBLEM | KEM | Lattice | LWE/RLWE | Discard | - | - | - | |
| Falcon | DSA | Lattice | Hash then sign | FIPS-206 | ||||
| FrodoKEM | KEM | Lattice | LWE | FrodoKEM | Discard | |||
| GeMSS | DSA | Multivariate | HFE | GeMSS | Discard | |||
| Giophantus | DSA | Symmetric | Hash | Discard | - | - | - | |
| Gravity-SPHINCS | DSA | Symmetric | Hash | Discard | - | - | - | |
| Guess Again | DSA | Lattice | Discard | - | - | - | ||
| GUI | DSA | Multivariate | HFE | Discard | - | - | - | |
| HILA5 | KEM | Lattice | RLWE | Round 5 | - | - | - | |
| HiMQ-3 | DSA | Multivariate | UOV | Discard | - | - | - | |
| HK17 | DSA | Multivariate | UOV | Withdrawn | Discard | - | - | - |
| HQC | KEM | Codes | Short Hamming | HQC | HQC | |||
| KCL (OKCN/AKCN/CNKE) | KEM | Lattice | LWE/RLWE/LWR | Discard | - | - | - | |
| KINDI | KEM | Lattice | MLWE | Discard | - | - | - | |
| LAC | KEM | Lattice | RLWE | Discard | - | - | ||
| LAKE | KEM | Codes | low rank | Rollo | Discard | - | ||
| LEDAkem | KEM | Codes | Short Hamming | LEDACrypt | Discard | - | - | |
| LEDApkc | KEM | Codes | Short Hamming | LEDACrypt | Discard | - | - | |
| Lepton | DSA | Codes | Discard | - | - | - | ||
| LIMA | KEM | Lattice | RLWE | Discard | - | - | - | |
| Lizard | KEM | Lattice | LWE/RLWE | Discard | - | - | - | |
| LOCKER | KEM | Codes | low rank | Rollo | Discard | - | ||
| LOTUS | KEM | Lattice | LWE | Discard | - | - | - | |
| LUOV | DSA | Multivariate | UOV | Discard | - | - | ||
| McNie | KEM | Lattice | Discard | - | - | - | ||
| Mersenne-756839 | KEM | Lattice | ILWE | Discard | - | - | - | |
| MQDSS | DSA | Multivariate | Fiat-Shamir | Discard | - | - | ||
| NewHope | KEM | Lattice | RLWE | Discard | - | - | ||
| NTRUEncrypt | KEM | Lattice | NTRU | NTRU | NTRU | NTRU | Discard | |
| NTRU-HRSS-KEM | KEM | Lattice | NTRU | NTRU | NTRU | NTRU | Discard | |
| NTRU Prime | KEM | Lattice | NTRU | NTRU Prime | Discard | |||
| NTS-KEM | KEM | Codes | Goppa | Classic McEliece | Classic McEliece | |||
| Odd Manhattan | KEM | Lattice | Lattice | Discard | - | - | - | |
| Ouroboros-R | KEM | Codes | low rank | Rollo | - | - | ||
| Picnic | DSA | Symmetric | ZKP | Picnic | Discard | |||
| Post-quantum RSA-Encryption | KEM | Factorization | Discard | - | - | - | ||
| Post-quantum RSA-Signature | DSA | Factorization | Discard | - | - | - | ||
| pqNTRUSign | DSA | Lattice | Hash then sign | Discard | - | - | - | |
| pqsigRM | DSA | Discard | - | - | - | |||
| QC-MDPCKEM | KEM | Codes | Short Hamming | Discard | - | - | - | |
| qTESLA | DSA | Lattice | Fiat-Shamir | Discard | - | - | ||
| RaCoSS | KEM | Lattice | Discard | - | - | - | ||
| Rainbow | DSA | Multivariate | UOV | Rainbow | Discard | |||
| Ramstake | KEM | Lattice | LWE | Discard | - | - | - | |
| RankSign | DSA | Codes | RSDP | Withdrawn | Discard | - | - | - |
| RLCE-KEM | KEM | Codes | RSDP | Discard | - | - | - | |
| Round2 | KEM | Lattice | LWE/RLWE | Round 5 | Discard | - | - | |
| RQC | KEM | Codes | low rank | Discard | - | - | ||
| RVB | KEM | Codes | Withdrawn | Discard | - | - | - | |
| SABER | KEM | Lattice | MLWE | SABER | Discard | |||
| SIKE | KEM | Isogeny | Isogeny | SIKE | SIKE | |||
| SPHINCS+ | DSA | Symmetric | Hash | FIPS 205 | ||||
| SRTPI | DSA | Symmetric | Hash | Withdrawn | Discard | - | - | - |
| ThreeBears | KEM | Lattice | IMLWE | Discard | - | - | ||
| Titanium | KEM | Lattice | MP-LWE | Discard | - | - | - | |
| WalnutDSA | DSA | Braid group | Discard | - | - | - |
Attachment: NIST Post-Quantum Cryptography: Additional Digital Signature Schemes
List of algorithms in the extended set of Additional Digital Signature Schemes, including details as in other contests. This contest extends the NIST PQC competition and should offer alternative digital signature schemes.
| Algorithm | Účel | Problem | Type | Round 1 | Round 2 | Round 3 |
| 3WISE | DSA | Multivariate | Discard | - | ||
| AIMer | DSA | Symmetric | Discard | - | ||
| Ascon-Sign | DSA | Symmetric | Discard | - | ||
| ALTEQ | DSA | Discard | - | |||
| Biscuit | DSA | MPC | Discard | - | ||
| CROSS | DSA | Linear code | ||||
| DME-Sign | DSA | Multivariate | Discard | - | ||
| EagleSign | DSA | Lattices | Discard | - | ||
| EHTv3 and EHTv4 | DSA | Lattices | Discard | - | ||
| EMLE-Sig 2.0 | DSA | Discard | - | |||
| Enhanced pqsigRM | DSA | Linear code | Discard | - | ||
| FAEST | DSA | Symmetric | ||||
| FuLeeca | DSA | Linear code | Discard | - | ||
| HAETAE | DSA | Lattices | Discard | - | ||
| HAWK | DSA | Lattices | ||||
| HPPC | DSA | Multivariate | Discard | - | ||
| HuFu | DSA | Lattices | Discard | - | ||
| KAZ-SIGN | DSA | Discard | - | |||
| LESS | DSA | Linear code | ||||
| MAYO | DSA | Multivariate | ||||
| MEDS | DSA | Linear code | Discard | - | ||
| MIRA | DSA | MPC | Mirath | |||
| MiRitH | DSA | MPC | Mirath | |||
| MQOM | DSA | MPC | ||||
| PERK | DSA | MPC | ||||
| Preon | DSA | Discard | - | |||
| PROV | DSA | Multivariate | Discard | - | ||
| QR-UOV | DSA | Multivariate | ||||
| Raccoon | DSA | Lattices | Discard | - | ||
| RYDE | DSA | MPC | ||||
| SDitH | DSA | MPC | ||||
| SNOVA | DSA | Multivariate | ||||
| SPINCS-Alpha | DSA | Symmetric | Discard | - | ||
| SQIsign | DSA | Isogeny | ||||
| SQUIRRELS | DSA | Lattices | Discard | - | ||
| TUOV | DSA | Multivariate | Discard | - | ||
| Xifrat1-Sign.I | DSA | Discard | - | |||
| UOV | DSA | Multivariate | ||||
| VOX | DSA | Multivariate | Discard | - | ||
| Wave | DSA | Linear code | Discard | - |
Note: MPC stands for Multi Party Computation, most of the listed algorithms meet the ZKP, i.e. the Zero Knowledge Principle.
Attachments: List of algorithms in the KpqC Competition
List of algorithms in the South Korean competition, including their details, similar to the NIST PQC competition. This overview is still not complete and the aim is to fill in the individual missing data to allow a preview on the whole development.
| Algorithm | Goal | Problem | Type | Submission | Round 1 | Round 2 |
| AlMer | DSA | |||||
| Enhanced pqsigRM | DSA | Hash | Discard | - | ||
| FIBS | DSA | Hash | Discard | - | ||
| GCKSign | DSA | Isogenies | Discard | - | ||
| HAETAE | DSA | Lattices | SVP/LWE | |||
| IPCC | KEM | Hash | Discard | - | ||
| Layered ROLLO-I | KEM | Codes | RSDP | Discard | - | |
| MQ-Sign | DSA | Multivariate | ||||
| NCC-Sign | DSA | |||||
| NTRU+ | KEM | Lattices | SVP | |||
| PALOMA | KEM | Lattices | LWE/RLWE | |||
| Peregrine | DSA | Multivariate | Discard | - | ||
| REDOG | KEM | Lattices | LWE/RLVE | |||
| SMAUG | KEM | Multivariate | SMAUG+TiGER | |||
| SOLMAE | DSA | Codes | SDP/ECCP | Discard | - | |
| TiGER | KEM | Multivariate | SMAUG+TiGER |
Attachments: List of algorithms in CACR contest PQC standardization
The contest was in two categories, the results are listed here. The list of algorithms is complete, but details
are missing for the time being. Therefore, it is tough to get an overview of the whole development and to determine
why some technologies were used and what type of technologies are involved. That will be added later.
Elected algorithms: AIGIS-SIG, LAC.PLE, AIGIS-ENC, LAC.KEX, SIAKE, SCloud, AKCN(AKCN-MLWE), OKCN(SKCN-MLWE), Fatseal, AKCN-E8, TALE, PKP-DSS, Piglet-1
| Algorithm | Goal | Problem | Type | Result |
| Aigis-enc | KEM | Lattices | LWE/SIS | Elected |
| Aigis-sig | DSA | Lattices | LWE/SIS | Elected |
| AKCN-E8 | KEM | Lattices | RLWE | Elected |
| AKCN-LWE | KEM | Lattices | LWE | Discard |
| AKCN-LWR | KEM | Lattices | LWR | Discard |
| AKCN-MLWE | KEM | Lattices | MLWE | Elected (AKCN) |
| CAKE | Discard | |||
| COLA | KEM | Lattices | CVP/LWE | Discard |
| D-NTRU | KEM | Lattices | CVP | Discard |
| ECC2 | KEM | Discard | ||
| ESS | DSA | Symetrické | HBS | Discard |
| FatSeal | KEM | Lattices | CVP | Elected |
| Gamma signatures and agregation algorithms for new applications and new formats of blockchain and financial payments | DSA | Discard | ||
| GoShine | KEM | Lattices | CVP | Discard |
| HEL exchange algorithm | KEM | Lattices | RLWE | Discard |
| HEL publick key encryption key encapsulation algorithm | KEM | Lattices | RLWE | Discard |
| Higncryption | DSA | Other | Discard | |
| LAC.KEX | KEM | Lattices | LWE | Elected |
| LAC.PKE | DSA | Lattices | LWE | Elected |
| LADAC | Discard | |||
| LAKA | KEM | Lattices | RLWE | Discard |
| LAKE | Discard | |||
| LASNET | DSA | Lattices | CVP/RLWE | Discard |
| Loong-1 | KEM | Linear codes | Goppa | Discard |
| Loong-2 | KEM | Linear codes | Goppa | Discard |
| Magnolia | Discard | |||
| NSG | DSA | Lattices | RLWE | Discard |
| OKCN-LWE | KEM | Lattices | RLWE | Discard |
| OKCN-LWR | KEM | Lattices | LWR | Discard |
| OKCN-SEC | KEM | Lattices | LWE | Discard |
| Piglet-1 | KEM | Linear codes | Goppa | Elected |
| Piglet-2 | KEM | Linear codes | Goppa | Discard |
| PKP-DSS Signature Scheme | DSA | Other | Elected | |
| SKCN-MLWE | KEM | Lattices | MLWE | Elected (OKCN) |
| SCLOUD | Elected | |||
| SIAKE | KEM | Isogenies | SIDH | Elected |
| Square-Free | KEM | Multivariate | Discard | |
| TALE | KEM | Lattices | SVP/RLWE | Elected |
Reference:
- Digital signature algorithm for use cases such as signing firmware and software.
Source: https://nvlpubs.nist.gov/ - RFC 8391: XMSS: eXtended Merkle Signature Scheme.
Source: https://www.rfc-editor.org/ - RFC 8554: Leighton-Micali Hash-Based Signatures.
Source: https://www.rfc-editor.org/ - RFC 9180: Hybrid Public Key Encryption.
Source: https://www.rfc-editor.org/ - After 60 years, another busy beaver problem solved.
Source: https://medium.com/ - FIPS 203 Module-Lattice-Based Key-Encapsulation Mechanism Standard.
Source: https://www.nist.gov/ - FIPS 204 Module-Lattice-Based Digital Signature Standard.
Source: https://www.nist.gov/ - FIPS 205 Stateless Hash-Based Digital Signature Standard.
Source: https://www.nist.gov/ - Open Quantum Safe.
Source: https://openquantumsafe.org/ - Post-Quantum Cryptography Alliance.
Source: https://pqca.org/ - Post-Quantum Cryptography Coallition.
Source: https://pqcc.org/ - QUBIP Transition of NSS and Firefox to support the quantum secure internet browsing.
Source: https://qubip.eu/ - Coordinated Implementation Roadmap for the transition to Post-Quantum Cryptography
Source: https://eur-lex.europa.eu/ - Post-Quantum Cryptography: Additional Digital Signature Schemes
Source: https://csrc.nist.gov/ - Post Quantum Government Initiatives by Country and Region
Source: https://www.gsma.com/ - PQC Capabilities Matrix (PQCCM)
Source: https://pkic.org/



